বিষয়ভিত্তিক যোগ্যতার বিবরণী
সংখ্যা, গণনা, জ্যামিতি, পরিমাপ ও তথ্য বিশ্লেষণের ধারণা আয়ত্তীকরণ ও ব্যবহারের মাধ্যমে ব্যক্তিগত, সামাজিক, জাতীয় ও বৈশ্বিক সমস্যার দ্রুত মূল্যায়ন করে কার্যকর যোগাযোগের মাধ্যমে বর্তমান সমস্যার সমাধান ও ভবিষ্যত সমস্যা সম্পর্কে করণীয় নির্ধারণ করতে পারা। এছাড়া গাণিতিক দক্ষতা ব্যবহার করে যৌক্তিক ও কল্যাণকর সিদ্ধান্ত নিতে পারা এবং উদ্ভাবনী সক্ষমতা প্রদর্শন ও প্রয়োগ করতে পারা।
বিষয়ের ধারণায়
গণিত এমন একটি চিন্তন প্রক্রিয়া যার মাধ্যমে বিমূর্ত ধারণাকে যৌক্তিকভাবে সম্পর্কযুক্ত করা হয়। তাই গণিতের মূল ভিত্তি যুক্তি ও সৃজনশীলতা। জটিল বৈজ্ঞানিক সমস্যা থেকে শুরু করে প্রাত্যহিক হিসাব নিকাশ পর্যন্ত গণিতের বিস্তৃতি দৃশ্যমান ।
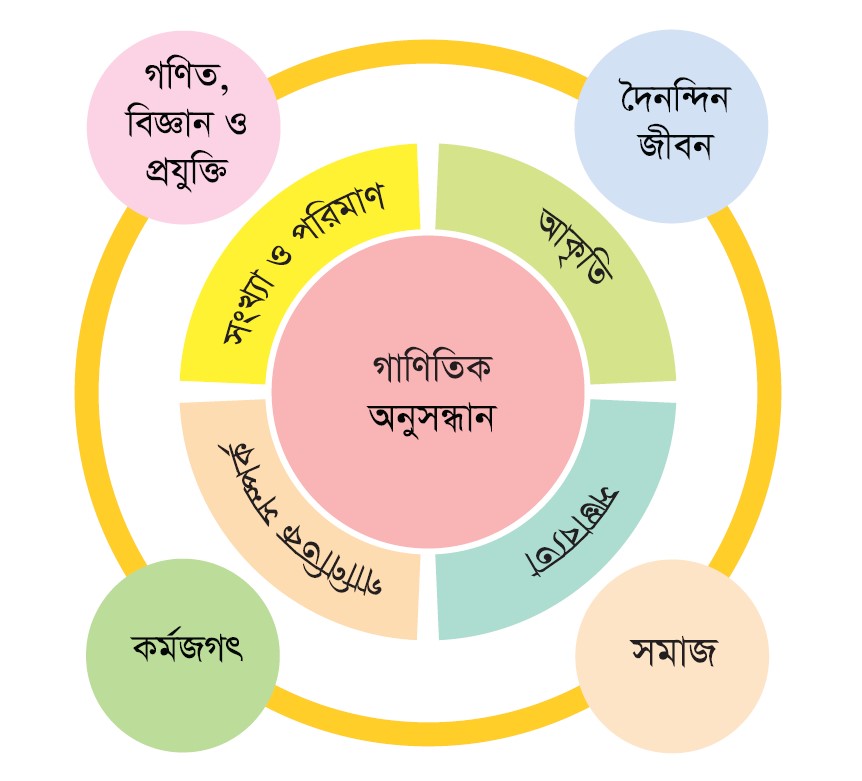
শিক্ষাক্রম রূপরেখা প্রণয়নের ক্ষেত্রে শুধু কিছু সূত্র মুখস্থ করে তার সাহায্যে পাঠ্যপুস্তকভিত্তিক সমস্যা সমাধান নয় বরং গণিতের প্রকৃতি, যৌক্তিক চিন্তন, বাস্তব জীবনে এগুলোর প্রয়োগ ইত্যাদির উপর জোর দেওয়া হয়েছে। সেজন্য এই বিষয়ের ধারণায়নের কেন্দ্রে রাখা হয়েছে গাণিতিক অনুসন্ধান, যে প্রক্রিয়ায় শিক্ষার্থীরা গাণিতিক দক্ষতা ও দৃষ্টিভঙ্গি ব্যবহার করে গণিতের বিভিন্ন ক্ষেত্রে সমস্যা সমাধানের যোগ্যতা অর্জন করবে। গণিতের বিভিন্ন ক্ষেত্র সম্পর্কে আলোচনা করার জন্য চারটি ডাইমেনশন নির্ধারণ করা হয়েছে, যেগুলো হল : সংখ্যা ও পরিমাণ, গাণিতিক সম্পর্ক, আকৃতি এবং সম্ভাব্যতা। এই চারটি ডাইমেনশনে গাণিতিক অনুসন্ধান চর্চার মাধ্যমে শিক্ষার্থীরা যে যোগ্যতাসমূহ অর্জন করবে তা সে তার জীবনের বিভিন্ন ক্ষেত্রে প্রয়োগ করতে পারবে। এসকল প্রয়োগক্ষেত্রকে চারটি মূল ভাগে ভাগ করা হয়েছে; যেমন : দৈনন্দিন জীবনে, সমাজ জীবনে, কর্মজ্ঞাতে এবং গণিতের উচ্চতর শিখন ও গবেষণাসহ বিজ্ঞান ও প্রযুক্তির ক্ষেত্রে।
গণিত বিষয়ের ধারণায়নে উঠে আসা সংশ্লিষ্ট বিষয়গুলো সম্পর্কে আরেকটু বিস্তারিতভাবে নিচে আলোকপাত করা হল ।
গাণিতিক অনুসন্ধান
গণিত বিষয়ের একটি মূল লক্ষ্য হলো গাণিতিক সাক্ষরতা- যা বাস্তব জীবনের কোনো সমস্যা সমাধানের জন্য কীভাবে সমস্যাকে পরিকল্পনা করতে হয় এবং এর একটি গাণিতিক রূপ দিয়ে তা ব্যাখ্যা ও সমাধান করা যায় সে ধরনের সক্ষমতা প্রদান করে। আর সমস্যা সমাধানের এই সুসংবদ্ধ প্রক্রিয়াকে বলা হয় গাণিতিক অনুসন্ধান । গণিত হচ্ছে যথার্থভাবে সংজ্ঞায়িত বস্তু এবং ধারণা সম্পর্কিত বিজ্ঞান, যেখানে গাণিতিক অনুসন্ধান প্রক্রিয়া ব্যবহার করে বিভিন্নভাবে বস্তু বা ধারণার ব্যাখ্যা ও রূপান্তরের মাধ্যমে একটি নিশ্চিত উপসংহারে পৌঁছানো সম্ভব হয় ।
বস্তুনিষ্ঠ ও গ্রহণযোগ্যভাবে যুক্তি উপস্থাপন একটি দক্ষতা। প্রযুক্তিনির্ভর এ বিশ্বে গুরুত্বপূর্ণ এ দক্ষতাটির চাহিদা ক্রমাগত বৃদ্ধি পাচ্ছে। গাণিতিক যুক্তি প্রয়োগ করে শিক্ষার্থীরা তাদের বাস্তব জীবনের সমস্যা সমাধানে এমন একটি ফলাফলে উপনীত হয় যেটিকে তারা পরিপ্রেক্ষিত বিবেচনা করে সঠিক বলে মনে করে। গাণিতিক অনুসন্ধান প্রক্রিয়া অনুসরণ করে গাণিতিক যুক্তি ব্যবহারের মাধ্যমে যে উপসংহারে পৌঁছানো যায় তা অনেক বেশি গ্রহণযোগ্য ও বস্তুনিষ্ঠ হয় এবং বাস্তব বা বিমূর্ত যেকোনো গাণিতিক সমস্যা সমাধানে এই প্রক্রিয়া অনুসরণ করতে হয়। এজন্য এই রূপরেখায় গাণিতিক অনুসন্ধানকে ধারণায়নের মডেলের কেন্দ্রে অবস্থান দেওয়া হয়েছে।
গাণিতিক অনুসন্ধানের আলোকে যে বিষয়গুলো উপলব্ধি করা যায় সেগুলো হলো :
- পরিমাণ, সংখ্যা-কাঠামো ও তাদের বীজগণিতীয় সম্পর্ক উপলব্ধি করা
- বিমূর্ত ধারণা ও তাদের প্রতীকীয় সৌন্দর্য উপভোগ ও কদর করা
- গাণিতিক গঠন এবং তাদের ধারাবাহিকতা দেখা
- রাশিসমূহের কার্যকর সম্পর্ক মেনে নেওয়া
- ভৌত, জীব, সামাজিক, অর্থনৈতিক এবং আচরণিক বিজ্ঞানের ক্ষেত্রে গাণিতিক মডেলকে লেন্স হিসেবে ব্যবহার করা
- পরিসংখ্যানের প্রাণ হিসেবে চলকের ভূমিকা উপলব্ধি করা (পিসা ২০২১ : গণিত ফ্রেমওয়ার্ক)
এবার আমরা গাণিতিক অনুসন্ধানের উপলব্ধিগুলোকে যদি বিশ্লেষণ করি তা হলে দুইটি গুরুত্বপূর্ণ দিক উঠে
আসে :
১. তাত্ত্বিক দিক : যার মধ্যে রয়েছে, সংখ্যা ও পরিমাণ, গাণিতিক সম্পর্ক, আকৃতি ও সম্ভাব্যতা।
২. ব্যবহারিক দিক : যার মধ্যে রয়েছে, বিজ্ঞান ও প্রযুক্তি, দৈনন্দিন জীবন, কর্মজগৎ ও সমাজ।
একজন শিক্ষার্থী গাণিতিক অনুসন্ধান করতে গিয়ে যে চারটি ডাইমেনশন বা ক্ষেত্রের ভেতর দিয়ে বিকশিত হবে তার একটি বর্ণনা নিচে তুলে ধরা হলো :
- সংখ্যা ও পরিমাণ
সংখ্যা একটি বিমূর্ত ধারণা। সংখ্যার সঙ্গে যখন পরিমাণ যুক্ত হয় তখন সংখ্যা বোধ তৈরি হয় । পরিমাণের ধারণা ছাড়া সংখ্যা ব্যাখ্যা সহজ নয় ।
আমরা যদি মহাবিশ্বের দিকে তাকাই তা হলে দেখতে পাই, মহাবিশ্ব হচ্ছে গ্যালাক্সি থেকে শুরু করে ক্ষুদ্রাতিক্ষুদ্র অসংখ্য অণু পরমাণুর মহাসাগর যেখানে বস্তুসমূহের ক্রিয়া প্রতিক্রিয়ায় তৈরি হচ্ছে বিভিন্ন ঘটনা। মহাবিশ্বের প্রতিটি বস্তুকণা এবং প্রতিটি সত্তার পারস্পরিক মিথস্ক্রিয়া এবং তার সৌন্দর্য উপভোগ করার জন্য সংখ্যা ও পরিমাণের ধারণা; অর্থাৎ সংখ্যা-বোধ হচ্ছে সবচেয়ে প্রয়োজনীয় গাণিতিক দিক, যা শিক্ষার্থীকে এই বিশাল জগতে প্রবেশের সুযোগ করে দেয়। এর সঙ্গে সংযোজিত হয়েছে মহাবিশ্বের নানা বস্তুকণার বৈশিষ্ট্য, সম্পর্ক ও অবস্থানকে সংখ্যার আলোকে প্রকাশ করা এবং পরিমাণের আলোকেই এ প্রকাশকে দেখার চেষ্টা করা। পরিমাণের এ ধারণা থেকে আমরা পরিমাপ, গণনা, বিস্তার, একক, নির্দেশক, আকৃতি, ক্রমিক সংখ্যার প্রবণতা ও প্যাটার্ন উপলব্ধি করি। হাজার হাজার বছর ধরে মানুষ প্রকৃতির এই ঐক্য ও শৃঙ্খলাকে বুঝতে চেষ্টা করেছে, এবং বহু প্রজন্মের চিন্তন, চর্চা, ও অক্লান্ত পরিশ্রমের মধ্য দিয়ে বিশ্বজাতের নিয়ম কানুনকে ব্যাখ্যা করার পথে ধীরে ধীরে এগোনোর চেষ্টা করেছে।
পৃথিবীর বিশালত্ব পরিমাপ এবং বর্ণনা করার জন্য তাকে সংখ্যায় প্রকাশ করা একটি প্রাথমিক প্ৰক্ৰিয়া । যা কোনো একটি অবস্থার মডেলিং, পরিবর্তন ও সম্পর্ক পরীক্ষণ, আকার আকৃতি এবং তথ্য সংগঠন ও অনিশ্চয়তা পরিমাপ করার অনুমতি প্রদান করে।
- গাণিতিক সম্পর্ক
প্রাকৃতিক ও কৃত্রিম জগতের বস্তু এবং পারিপার্শ্বিকতার মধ্যে বহু ধরনের স্থায়ী ও অস্থায়ী সম্পর্ক দেখা যায়। যেখানে একটি সিস্টেমের ভেতর ঘটে চলা বস্তুসমূহের পরিবর্তন অথবা পারিপার্শ্বিকতায় একটি উপাদান আর একটি উপাদানকে কীভাবে প্রভাবিত করছে তা দেখা যায়। অনেক ক্ষেত্রেই এ পরিবর্তন দীর্ঘ কিংবা অল্প সময়ব্যাপী সংঘটিত হয়। আবার অন্য ক্ষেত্রে একটি বস্তু বা পরিমাণ অন্যটির পরিবর্তনের সঙ্গে সম্পর্কিত। কোনো ক্ষেত্রে পরিবর্তন হয় আলাদা আলাদা আবার কখনো কখনো তা নিরবিচ্ছিন্নভাবে হয়ে থাকে। এই সম্পর্কগুলো কখনো কখনো প্রকৃতিতে দীর্ঘস্থায়ী এবং অপরিবর্তনীয় । গাণিতিক মডেলের আলোকে এ পরিবর্তন পূর্বানুমান ও ব্যাখ্যা করা যায়। অর্থাৎ গাণিতিকভাবে পরিবর্তন এবং সম্পর্ককে যথ াযথ ফাংশন এবং সমীকরণের সাহায্যে মডেলিং করা যায়। এই মডেলই বাস্তব জীবনের কোনো ঘটনাকে প্রতীক বা গ্রাফের মাধ্যমে প্রকাশ করে থাকে ।
- আকৃতি
আমরা আমাদের দৃশ্যমান জগতে প্রতিনিয়ত আকার আকৃতি সম্পর্কিত প্রপঞ্চের (phenomena) সম্মুখীন হই যেমন; জ্যামিতিক প্যাটার্ন, বস্তুর বিভিন্ন বৈশিষ্ট্য, অবস্থান এবং ওরিয়েন্টেশন, বস্তুর উপস্থাপন, দৃশ্যমান তথ্যের কোডিং এবং ডিকোডিং, বাস্তব আকৃতির সঙ্গে মিথষ্ক্রিয়া ইত্যাদি। জ্যামিতিক ধারণা আকার আকৃতির ব্যাখ্যায় ভিত তৈরি করলেও পরিমাপ এবং বীজগণিতের ধারণায়নেও জ্যামিতির ভূমিকা রয়েছে।
আমরা সচরাচর যে ধরনের আকৃতি দেখতে পাই তা প্রতিসম (symmetrical) নয়। তাই জ্যামিতির সহজ সূত্রের সাহায্যে এ ধরনের অনিয়মিত আকৃতি পরিমাপ করা জটিল । কাজেই আকৃতির পরিমাপের ক্ষেত্রে একটি কাছাকাছি ফলাফলের উপরই নির্ভর করতে হয়। এক্ষেত্রে যতটা ত্রুটিমুক্ত করা সম্ভব তা করা হয়ে থাকে ।
- সম্ভাব্যতা
বিজ্ঞান, প্রযুক্তি, প্রাত্যহিক জীবন বা সমাজে সম্ভাব্যতা বা অনিশ্চয়তাকে উপেক্ষা করা যায় না। তাই সম্ভাব্যতা বা অনিশ্চয়তা গাণিতিক ব্যাখ্যার একটি উল্লেখযোগ্য অনুষঙ্গ। গাণিতিক সমস্যা সমাধানের ক্ষেত্রে, সম্ভাব্যতা যাচাই, তথ্য উপস্থাপন এ সব ক্ষেত্রই অনিশ্চয়তার ঘটনা একটি মুখ্য ভূমিকা পালন করে।
স্বাস্থ্যঝুঁকি নির্ধারণ, নির্বাচনী মতামত, জনসংখ্যার প্রবণতা ইত্যাদি উপস্থাপনে গ্রাফ ও পরিসংখ্যান একটি গুরুত্বপূর্ণ স্থান জুড়ে আছে। প্রতিটি ক্ষেত্রই একটি সম্ভাব্য ফলাফলের উপর আলোকপাত করে। ডাটা সংগ্রহ, ব্যবস্থাপনা এবং তথ্য বিশ্লেষণ করে সম্ভাব্যতা উপস্থাপন করাই এক্ষেত্রে গুরুত্বপূর্ণ ।
উল্লেখিত চারটি ডাইমেনশনের আলোকে অর্জিত গাণিতিক সাক্ষরতা একজন শিক্ষার্থী প্রেক্ষাপটভেদে সমস্যা সমাধানে প্রয়োগ করতে পারছে কিনা এটা খুবই গুরুত্বপূর্ণ । নিচে এই প্রয়োগের চারটি প্রধান ক্ষেত্ৰ তুলে ধরা হলো :
- গণিত, বিজ্ঞান ও প্রযুক্তি
গণিতের বিভিন্ন ক্ষেত্রে উচ্চতর শিখন ও গবেষণাসহ বিজ্ঞান ও প্রযুক্তির বিভিন্ন ক্ষেত্র; যেমন : আবহাওয়া ও জলবায়ু, বাস্তুসংস্থান, মহাকাশ বিজ্ঞান, ওষুধ প্রস্তুত, জেনেটিক্স ইত্যাদি নানা ক্ষেত্রে গাণিতিক সাক্ষরতার প্রয়োগ প্রয়োজন হয়।
- দৈনন্দিন জীবন
দৈনন্দিন জীবনে নানা ক্ষেত্রে মানুষকে প্রতিনিয়ত গণিতের ব্যবহার করতে হয়। যেমন : খাবার প্রস্তুত, ক্রয়-বিক্রয়, ব্যক্তিগত স্বাস্থ্য, যাতায়াত, ভ্রমণ, প্রতিদিনের কাজের সূচি তৈরি ইত্যাদি ।
- কর্মজগত
কর্মজ্ঞাতের অনেক সমস্যা সমাধানে গণিতের ধারণা ব্যবহার করতে হয়। যেমন : পরিমাপ, বাজেট প্রণয়ন, হিসাব নিকাশ, মান নিয়ন্ত্রণ, অফিস সময়সূচি, বর্ণনামূলক তালিকা, নকশা প্রণয়ন, চাকুরি সংক্রান্ত সিদ্ধান্ত গ্রহণ ইত্যাদি সকল ক্ষেত্রে গণিতের ব্যবহার প্রণিধানযোগ্য।
- সমাজ
সামাজিক পরিপ্রেক্ষিত; যেমন : স্থানীয়, জাতীয় ও আন্তর্জাতিক প্রেক্ষাপটে বিভিন্ন সমস্যা সমাধানে গণিতের জ্ঞান প্রয়োগ করতে হয়। যেমন : নির্বাচন-ব্যবস্থা, গণপরিবহণ, সরকার, জনমিতি, বিজ্ঞপ্তি প্রদান, জাতীয় পরিসংখ্যান, অর্থনীতি ইত্যাদি।
===000===
তথ্যসূত্র : শিক্ষাক্রম রুপরেখা-2021
